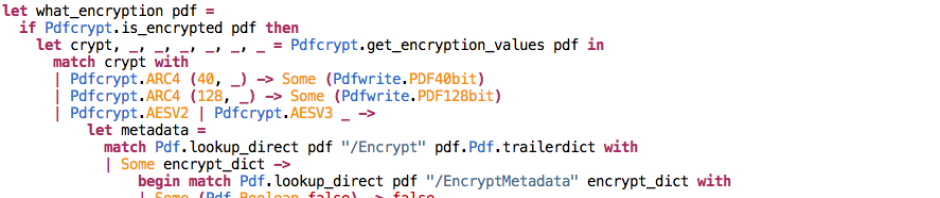
For rendering vector graphics scenes, colours are usually stored with what we call “premultiplied” or “associated” alpha. For instance, opaque dark red is stored as:
0.5, 0, 0, 0.5 (R * A, G * A, B * A, A)
instead of
0.5, 0, 0, 1 (R, G, B, A).
This originally had to do with making compositing algorithms fast (fewer multiplications), but it has other advantages – for instance there is only a single value for the clear colour (0, 0, 0, 0) instead of many (x, y, z, 0).
We usually use 8 bits for each component, packing them into a 32 bit word.
Now, 32 bits can store 2^32 colours. In fact, in the premultiplied scheme, many bit patterns are unused (when R, G or B is > A). It turns out there are only slightly more than 2^30 unique premultiplied colours. In other words, with a suitable mapping, we should be able to store them in OCaml’s 31 bit integers. This is important so we can store them in native arrays unboxed, for example.
Such a mapping (togther with a discussion of all this) is in Jim Blinn’s book “Dirty Pixels”, Chapter 20. Unfortunately, it’s too slow for practical use. Can you think of a fast one?
Meanwhile, here’s some code from our renderer which uses a lossy approach: throwing away the least significant red bit (The question of which colour to lose the bit is not clear: theoretically the eyes are less sensitive to changes in blue, but my tests didn’t seem to bear that out).
To build one of these colours (assertions left out for this post)
let colour_of_rgba r g b a =
(a lsl 23) lor (b lsl 15) lor (g lsl 7) lor (r lsr 1)
Extraction of blue, green and alpha components is easy, but where we’ve dropped the LSB, we need to reconstruct carefully, at least making sure 254 reconstructs to 255 – otherwise we couldn’t represent full red. We must also make sure the invariant that a component can never be more than the alpha is obeyed.
let rec red_of_colour c =
let red =
match (c land 127) lsl 1 with
| 254 -> 255
| r -> r
and alpha = c lsr 23 in
if red > alpha then alpha else red
In Part Two, I’ll release the Colour module, which provides for all this, and implements the standard Porter/Duff compositing arithmetic efficiently.